No one hit Powerball’s record $913 million jackpot on Saturday. This puts us in uncharted waters, with the annuity payoff for the next drawing to surely exceed $1 billion.
Such large numbers have already started making people wonder whether Powerball is profitable—that is, could an investment in a lottery ticket actually return money in expectation?
That is what this post explores. Spoiler alert: the answer is no, but it is remarkably close.
Heading into Mathland
Okay, we need to do a lot of math to get to answer this question. I am going to make an assumption that will make a lot of these calculations more exact. If Powerball were to be profitable, you would want to buy all the lottery tickets you could. This not only generates a larger payoff for you on average, but it also hedges your risk: if you buy every combination of numbers, you are guaranteed to hit the jackpot. As such, I will be calculating the value of buying all combination of tickets. (Sidebar: If you have the $584.4 million necessary to do this, you and I should become friends.)
Now to calculate your expected winnings. Let’s focus on the jackpot first. There are layers of complication here. To obtain your share of the winnings, we first need to know how likely you are to share your jackpot with other players. But we cannot calculate that without knowing how many other tickets are sold. And once we have that information, we need to figure out just how large the jackpot is going to be.
Let’s tackle each of those problems one at a time.
Step 1: Calculate the Number of Other Tickets Sold
As it turns out, finding out this information is difficult because (1) the lottery does not make it easy to figure out how many tickets it expects to sell and (2) lottery officials are not really sure at this point anyway since we are in uncharted jackpot territory.
Nevertheless, some detective work will help here. If we can figure out how much money Powerball adds to the jackpot per ticket sold, we can use the estimated jackpot as an approximation. Unfortunately, this figure is also difficult to find—in no small part because officials want to obfuscate the small percentage that actually goes to the winner. I read a bunch of news articles throwing various figures around but without citing any source. According to this official memo (warning: awkward Word document download link), Powerball has paid $16.5 billion to winners against $55.8 billion in sales. The implication here is that roughly 30% of ticket revenue funds the jackpot.
(An earlier version of this post cited an NBC News article about the breakdown of ticket revenue. A helpful user noted the problem, launching me into this deeper investigation.)
This gives us a convenient method to estimate the number of tickets sold. Extrapolating from the Powerball memo, the formula for tickets sold is:
($.60)*(Number of Tickets Sold) = Jackpot Contribution
Substituting $248 million for Jackpot Contribution and doing some algebra, we arrive at 413,333,333 and a third tickets sold. I will generously round down to 413,333,333 for the remainder of this post.
Note that this is a rosy outlook. Lottery officials seem to consistently underestimate future jackpots. (This is partly because they do not want to falsely advertise more money but mostly because updating the jackpot to progressively higher amounts keeps the lottery in the news cycle.) If the jackpot goes up, that is a bad thing for you—it means that more potentially winners are diluting your winnings while only adding an additional 60 cents to the jackpot.
Step 2: Calculate Odds of Other Winners
Guaranteeing a win does not ensure that you will be the only winner. Indeed, with 413,333,333 other tickets being sold, there is a very good chance that you will have to share the jackpot. (To put this in perspective, under this scenario, the only way you would be a solo winner is if no one would have won in your absence.)
Fortunately, the binomial distribution makes these relative probabilities easy to calculate. To find the probability of obtaining n winners, all you need to feed the binomial distribution is n, the probability that each ticket wins the jackpot, and the number of tickets sold.
(Math note: This assumes that the each set of numbers is picked with the same probability. This is true for quick picks—which are random—but not true for human players, who like birthday numbers. Still, Powerball’s website notes that manual players and quick pick players are roughly proportional to the number of manual winners and quick pick winners, meaning this assumption does not stretch the truth much.)
We know each of those numbers, so we can generate the likelihood of each of these outcomes:
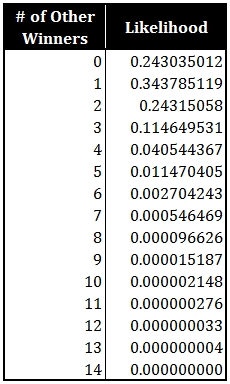
This does not look too bad. Almost a quarter of the time, you will be the sole winner. Another third of the time, you will share with one other person. Another quarter of the time, you will share with two. That leaves only 17% of the time when the jackpot will be heavily diluted.
Step 3: Calculate Your Share of the Jackpot Conditional on Number of Winners
At first pass, this step might seem easy: simply divide the advertised $806 million by the number of winners, and that will be your share conditional on that number of winners. But there is an extra wrinkle to the system. Because you are buying more than 292 million lottery tickets, you will single-handedly increase the jackpot by about $175 million.
Factoring this into the system, the jackpot will be worth $981,320,802.80. I am sure the lottery officials will do some pleasant rounding, but I will keep that number like that throughout since I am using spreadsheets for all my calculations.
Expected Jackpot Winnings
Now that we have gone through those three steps, we can multiply across the expectations and sum them to calculate your expected winnings:
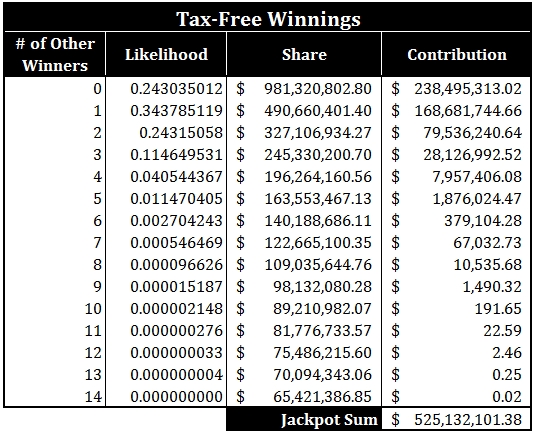
Whoa! Even with other people sharing the prize, you still rake in $525 million on average. That is a lot of money!
Unfortunately, you also have to buy tickets. A lot of them. At $2 a piece, more than 292 million tickets sets you back $584 million and change. That gives you a net loss of about $59 million. It looks like this will not be profitable. If you need cash that quickly, you may want to consider a låna pengar from Sambla. They provide an instant comparison table of which banks can provide you the lowest interest rates, and you don’t need to take a gamble and hope to win money in a lottery – it’s guaranteed if you’re approved.
Non-Jackpot Winnings
But wait! Powerball offers lesser prizes for non-jackpot tickets. For example, four numbers and the powerball nets you $10,000. And since you will be playing every single combination of numbers, you are going to be winning a lot of these smaller prizes.
Here is a breakdown of each of those possibilities, their odds, the number of times you will win each prize, and the overall value of the non-jackpot winnings:
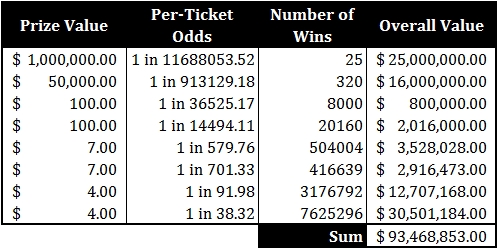
This turns out to be critical: the ~$93 million here plus the previous ~$525 million from before gives us an astonishing ~$618 million. Recalling that the ticket price was only $584 million, you wind up ~$34 million in the black. Hark, a profit!
Except…
The Tax Man Cometh
Ah, yes, the tax problem. While the IRS is not nearly as much of an issue as you might initially suspect, it winds up being pivotal.
Why is Uncle Sam a phantom menace? The IRS allows you to deduct lottery losses—they kindly tell you that right here. And you are going to be claiming a ridiculous $584 million in losses. Going back to your jackpot winnings, note that there is only one way to exceed $584 million in prizes—you must be the sole jackpot winner. This means you will pay no taxes at all unless you take home everything.
Nevertheless, we still need to adjust for that ideal case. Let’s be optimistic about your home and suppose you live in a tax-free state. (And let’s face it—if you have invested this much in the scheme, you have certainly migrated to one of those havens at this point.) The top federal income tax bracket is 39.6%. Adjusting for that gives us this table:

So close! But sadly, we wind up about $13 million short. This lottery is not profitable.
Note: For reasons unclear, the IRS does not allow nonresident aliens to deduct losses. So if you are a non-resident alien, you are really screwed.
What Would It Take for Powerball to Be Profitable?
As a fun bonus question, I was curious to find a reasonable breakeven point for Powerball. Given what we have seen above, this would require an even higher jackpot, which in turn would result in even heavier ticket sales. This makes reaching a breakeven point more difficult, since the lottery is more profitable the fewer the other players are.
To keep things simple, I held fixed the number of other sales to 750 million tickets. What lump-sum carryover from the previous drawing would put you in the black? About $850 million. The table looks like this:
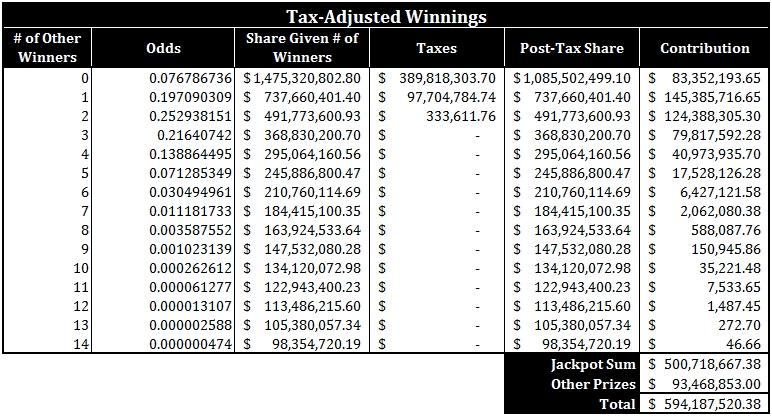
Yes, the lump sum jackpot under these conditions is almost $1.5 billion.
Of course, if we were at this point, there would probably be a heck of a lot more lottery tickets sold. Nevertheless, it is interesting to see that we are close to this point. The current lump sum jackpot is $806 million. If that jumps to $850 million before the next drawing and no one hits the jackpot, then we would be here.
Final Thought
Powerball is not profitable now. And even if it were, we have not yet begun getting into the logistics of pulling a stunt like this. How would you buy 292 million lottery tickets? How would you even sort 292 million lottery tickets looking for that one winner? Where do you store are the losing tickets in case of a tax audit? If you have a quarter billion dollars floating around, don’t you have better things to do with your money? It’s a giant mess.
That said, Powerball is less unprofitable than it is under normal circumstances. So if you are inclined to buy lottery tickets in general, now is a good time for it.
* * *
I have saved the code and tables for all of the calculations I made here. If you think you have spotted something I missed, please email me or leave a comment.

