I will assume that most readers are familiar with Hotelling’s game/the median voter theorem game. If not, the basic idea is that two ice cream vendors are on a beach that stretches the 0-1 interval. Customers are uniformly distributed along that interval. The vendors simultaneously select a position. Customers go to the closest vendor and split themselves evenly if the vendors choose an identical position. Each vendors want to maximize its number of customers.
(You can reframe the question as two candidates placing themselves along an ideological spectrum, with citizens voting for whichever one is closest.)
The Nash equilibrium is for both vendors to select the median location (.5); doing this guarantees each vendor half the business, but deviating to any other point generates strictly less. Full details here:
Proposition. For n even number of players, the following is a pure strategy Nash equilibrium to Hotelling’s game. Exactly two players choose each of these locations: 1/n, 3/n, …, (n-1)/n.
So, for example, for n = 2, two players occupy the position 1/2. (This is the median voter theorem.) For n = 4, two players occupy 1/4 and two players occupy 3/4. (No one occupies the median!) For n = 6, two players occupy 1/6, two players occupy 3/6, and two players occupy 5/6. (The median is back!) And so forth.
This has two interesting implications. First, the median voter theorem basically disappears. In half of these cases (i.e., when n/2 is itself even), no player occupies the median at all. In the other half of the cases, only two do. And even then, as n increases, the percentage of total players occupying the median goes to 0.
Second, quality of life for consumers is greatly enhanced compared to the n = 2 version of the game. Under those circumstances, some consumers would have to travel a full half-interval to reach one of the ice cream vendors. But as n increases, the vendors progressively spread out more and more. Things aren’t perfect—the vendors could spread out further (out of equilibrium) by dividing themselves uniformly—but it’s a step up if you previously thought that all of the vendors would take the median.
Proof
The proof isn’t terribly insightful, but here goes. In equilibrium, each individual earns a payoff of 1/n. This is because each position attracts 1/n customers on either side of the position. That 2/n sum is divided two ways for the two players occupying the position, so each earns 1/n.
The rest of the proof involves showing that there are no profitable deviations. There are three cases to consider. First, consider deviating to any other occupied position. Now three individuals are placed at the same spot. Their collective domains remains only 2/n portion of the interval. This is now split three ways, giving the individual a payoff of 2n/3, which is strictly less than 1/n.
Second, consider a deviation to a position beyond one of the more extreme locations—i.e., less than 1/n or greater than (n-1)/n. The argument is symmetric, so I will only consider an amount less than 1/n. Let x < 1/n be the deviation position. Consider the following hastily made but nonetheless helpful figure:
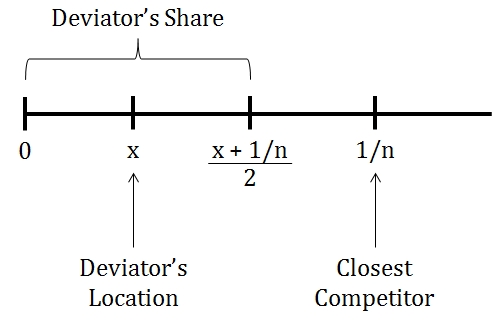
Because customers go to the closest location, the deviator takes all the customers between 0 and x as well as all customers to the left of the midpoint between x and 1/n, which is (x + 1/n)/2. The picture clearly shows that this is not a profitable deviation: the deviator’s share is now strictly smaller than the interval between 0 and 1/n, which is how much the deviator would have received if he stayed put. (Some algebra quickly verifies this.)
Finally, consider a deviation to a position between two locations already being occupied. Formally, we can describe this as any position between (m+1)/n and (m+3)/n, for any even integer m. For example, that could be any spot between 1/n and 3/n, 3/n and 5/n, and so forth. Letting y be the deviator’s new position, here’s another hastily made but helpful figure:

Now the deviator’s captured customers are bounded on the left of the midpoint between (m+1)/n and y and bounded on the right by the midpoint between y and (m+3)/n. It takes some algeabra to show, but this winds up being exactly equal to 1/n. In other words, the deviation isn’t profitable.
That exhausts all possible deviations. None are profitable, and thus this is a Nash equilibrium.
End
A couple notes. First, this doesn’t extend to odd cases, which tend to have…well…odd solutions. Second, there are other Nash equilibria for an even number of players, including some weird mixing.

